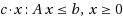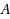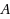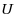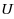| Article ID: | iaor20163631 |
| Volume: | 66 |
| Issue: | 2 |
| Start Page Number: | 195 |
| End Page Number: | 223 |
| Publication Date: | Oct 2016 |
| Journal: | Journal of Global Optimization |
| Authors: | Soyster A, Murphy F |
| Keywords: | programming: linear, heuristics |
The usual formulation of a linear program is max