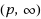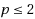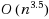Iterated local search with Trellis-neighborhood for the partial Latin square extension problem

A partial Latin square (PLS) is a partial assignment of n symbols to an $n\times n$ grid such that, in each row and in each column, each symbol appears at most once. The PLS extension problem is an NP‐hard problem that asks for a largest extension of a given PLS. We consider the local search such that the neighborhood is defined by (p, q)‐swap , i.e., the operation of dropping exactly p symbols and then assigning symbols to at most q empty cells. 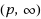As a fundamental result, we provide an efficient $(p,\infty )$ ‐neighborhood search algorithm that finds an improved solution or concludes that no such solution exists for $p\in \{1,2,3\}$ . The running time of the algorithm is $O(n^{p+1})$ . We then propose a novel swap operation, Trellis‐swap, which is a generalization of (p, q)‐swap with $p\le 2$ . 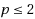The proposed Trellis‐neighborhood search algorithm runs in 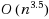$O(n^{3.5})$ time. The iterated local search (ILS) algorithm with Trellis‐neighborhood is more likely to deliver a high‐quality solution than not only ILSs with $(p,\infty )$ ‐neighborhood but also state‐of‐the‐art optimization solvers such as IBM ILOG CPLEX and LocalSolver.