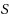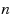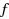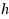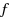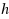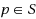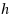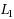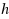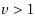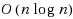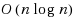| Article ID: | iaor20163543 |
| Volume: | 246 |
| Issue: | 1 |
| Start Page Number: | 167 |
| End Page Number: | 179 |
| Publication Date: | Nov 2016 |
| Journal: | Annals of Operations Research |
| Authors: | Ventura I, Prez-Lantero P, Daz-Bez J, Korman M |
| Keywords: | combinatorial optimization, design, location |
In this paper we extend the