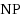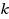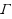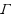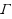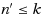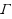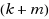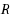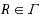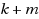The workflow satisfiability problem (wsp) is a problem of practical interest that arises whenever tasks need to be performed by authorized users, subject to constraints defined by business rules. We are required to decide whether there exists a plan–an assignment of tasks to authorized users–such that all constraints are satisfied. The wsp is, in fact, the conservative constraint satisfaction problem (i.e., for each variable, here called task, we have a unary authorization constraint) and is, thus,
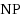 ‐complete. It was observed by Wang and Li (ACM Trans Inf Syst Secur 13(4):40, 2010) that the number
‐complete. It was observed by Wang and Li (ACM Trans Inf Syst Secur 13(4):40, 2010) that the number
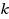 of tasks is often quite small and so can be used as a parameter, and several subsequent works have studied the parameterized complexity of wsp regarding parameter
of tasks is often quite small and so can be used as a parameter, and several subsequent works have studied the parameterized complexity of wsp regarding parameter
 . We take a more detailed look at the kernelization complexity of wsp(
. We take a more detailed look at the kernelization complexity of wsp(
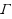 ) when
) when
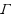 denotes a finite or infinite set of allowed constraints. Our main result is a dichotomy for the case that all constraints in
denotes a finite or infinite set of allowed constraints. Our main result is a dichotomy for the case that all constraints in
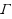 are regular: (1) We are able to reduce the number
are regular: (1) We are able to reduce the number
 of users to
of users to
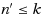 . This entails a kernelization to size poly
. This entails a kernelization to size poly
 for finite
for finite
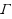 , and, under mild technical conditions, to size poly
, and, under mild technical conditions, to size poly
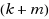 for infinite
for infinite
 , where
, where
 denotes the number of constraints. (2) Already wsp(
denotes the number of constraints. (2) Already wsp(
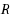 ) for some
) for some
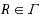 allows no polynomial kernelization in
allows no polynomial kernelization in
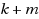 unless the polynomial hierarchy collapses.
unless the polynomial hierarchy collapses.