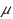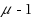MMAS Versus Population-Based EA on a Family of Dynamic Fitness Functions

We study the behavior of a population‐based EA and the Max–Min Ant System (MMAS) on a family of deterministically‐changing fitness functions, where, in order to find the global optimum, the algorithms have to find specific local optima within each of a series of phases. In particular, we prove that a (2+1) EA with genotype diversity is able to find the global optimum of the Maze function, previously considered by Kötzing and Molter [9], in polynomial time. This is then generalized to a hierarchy result stating that for every $\mathit{\mu }$ , a ( $\mathit{\mu }$ +1) EA with genotype diversity is able to track a Maze function extended over a finite alphabet of $\mathit{\mu }$ symbols, whereas population size $\mathit{\mu }-1$ is not sufficient. Furthermore, we show that MMAS does not require additional modifications to track the optimum of the finite‐alphabet Maze functions, and, using a novel drift statement to simplify the analysis, reduce the required phase length of the Maze function.