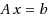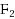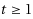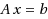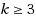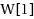| Article ID: | iaor20162564 |
| Volume: | 75 |
| Issue: | 2 |
| Start Page Number: | 322 |
| End Page Number: | 338 |
| Publication Date: | Jun 2016 |
| Journal: | Algorithmica |
| Authors: | Arvind V, Kbler Johannes |
| Keywords: | heuristics, programming: linear |
Given a system of linear equations