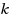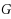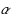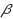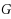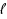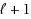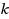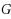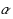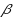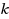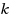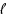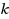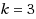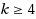The
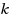 ‐colouring reconfiguration problem asks whether, for a given graph
‐colouring reconfiguration problem asks whether, for a given graph
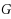 , two proper
, two proper
 ‐colourings
‐colourings
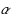 and
and
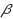 of
of
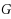 , and a positive integer
, and a positive integer
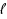 , there exists a sequence of at most
, there exists a sequence of at most
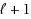 proper
proper
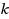 ‐colourings of
‐colourings of
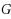 which starts with
which starts with
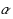 and ends with
and ends with
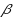 and where successive colourings in the sequence differ on exactly one vertex of
and where successive colourings in the sequence differ on exactly one vertex of
 . We give a complete picture of the parameterized complexity of the
. We give a complete picture of the parameterized complexity of the
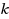 ‐colouring reconfiguration problem for each fixed
‐colouring reconfiguration problem for each fixed
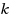 when parameterized by
when parameterized by
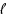 . First we show that the
. First we show that the
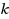 ‐colouring reconfiguration problem is polynomial‐time solvable for
‐colouring reconfiguration problem is polynomial‐time solvable for
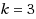 , settling an open problem of Cereceda, van den Heuvel and Johnson. Then, for all
, settling an open problem of Cereceda, van den Heuvel and Johnson. Then, for all
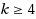 , we show that the
, we show that the
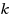 ‐colouring reconfiguration problem, when parameterized by
‐colouring reconfiguration problem, when parameterized by
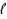 , is fixed‐parameter tractable (addressing a question of Mouawad, Nishimura, Raman, Simjour and Suzuki) but that it has no polynomial kernel unless the polynomial hierarchy collapses.
, is fixed‐parameter tractable (addressing a question of Mouawad, Nishimura, Raman, Simjour and Suzuki) but that it has no polynomial kernel unless the polynomial hierarchy collapses.