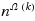In this paper we prove a space lower bound of
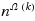for non‐deterministic (syntactic) read‐once branching programs (nrobps) on functions expressible as cnfs with treewidth at most k of their primal graphs. This lower bound rules out the possibility of fixed‐parameter space complexity of nrobps parameterized by k. We use lower bound for nrobps to obtain a quasi‐polynomial separation between Free Binary Decision Diagrams and Decision Decomposable Negation Normal Forms, essentially matching the existing upper bound introduced by Beame et al. (Proceedings of the twenty‐ninth conference on uncertainty in artificial intelligence, Bellevue, 2013) and thus proving the tightness of the latter.
