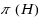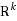| Article ID: | iaor20162559 |
| Volume: | 75 |
| Issue: | 1 |
| Start Page Number: | 187 |
| End Page Number: | 204 |
| Publication Date: | May 2016 |
| Journal: | Algorithmica |
| Authors: | Basavaraju Manu, Chandran L, Golumbic Martin, Mathew Rogers, Rajendraprasad Deepak |
| Keywords: | optimization |
Separation dimension of a hypergraph