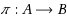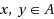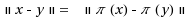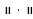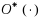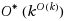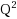We study the parameterized complexity of Geometric Graph Isomorphism (Known as the Point Set Congruence problem in computational geometry): given two sets of n points A and B with rational coordinates in k‐dimensional euclidean space, with k as the fixed parameter, the problem is to decide if there is a bijection
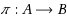 such that for all
such that for all
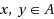 ,
,
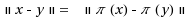 , where
, where
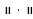 is the euclidean norm. Our main result is the following: We give a
is the euclidean norm. Our main result is the following: We give a
 time (The
time (The
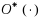 notation here, as usual, suppresses polynomial factors) FPT algorithm for Geometric Isomorphism. This is substantially faster than the previous best time bound of
notation here, as usual, suppresses polynomial factors) FPT algorithm for Geometric Isomorphism. This is substantially faster than the previous best time bound of
 for the problem (Evdokimov and Ponomarenko in Pure Appl Algebra 117–118:253–276, 1997). In fact, we show the stronger result that even canonical forms for finite point sets with rational coordinates can also be computed in
for the problem (Evdokimov and Ponomarenko in Pure Appl Algebra 117–118:253–276, 1997). In fact, we show the stronger result that even canonical forms for finite point sets with rational coordinates can also be computed in
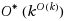 time. We also briefly discuss the isomorphism problem for other
time. We also briefly discuss the isomorphism problem for other
 metrics. Specifically, we describe a deterministic polynomial‐time algorithm for finite point sets in
metrics. Specifically, we describe a deterministic polynomial‐time algorithm for finite point sets in
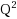 .
.