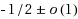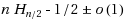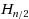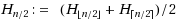The Impact of Random Initialization on the Runtime of Randomized Search Heuristics

Analyzing the runtime of a Randomized Search Heuristic (RSH) by theoretical means often turns out to be rather tricky even for simple optimization problems. The main reason lies in the randomized nature of these algorithms. Both the optimization routines and the initialization of RSHs are typically based on random samples. It has often been observed, though, that the expected runtime of RSHs does not deviate much from the expected runtime when starting in an initial solution of average fitness. Having this information a priori could greatly simplify runtime analyses, as it reduces the necessity of analyzing the influence of the random initialization. Most runtime bounds in the literature, however, do not profit from this observation and are either too pessimistic or require a rather complex proof. In this work we show for the two search heuristics Randomized Local Search (RLS) and the (1+1) Evolutionary Algorithm on the two well‐studied problems OneMax and LeadingOnes that their expected runtimes indeed deviate by at most a small additive constant from the expected runtime when started in a solution of average fitness. For RLS on OneMax, this additive discrepancy is $-1/2\pm o(1)$ , leading to the first runtime statement for this problem that is precise apart from additive o(1) terms: The expected number of iterations until an optimal search point is found, is $n{H}_{n/2}‐1/2\pm o(1)$ , where $H_{n/2}$ denotes the (n / 2)th harmonic number when n is even, and $H_{n/2}:=(H_{\lfloor n/2\rfloor }+H_{\lceil n/2\rceil })/2$ when n is odd. For this analysis and the one of the (1+1) EA optimizing OneMax we use a coupling technique, which we believe to be interesting also for the study of more complex optimization problems. For the analyses of the LeadingOnes test function, we show that one can express the discrepancy solely via the waiting times for leaving fitness level 0 and 1, which then easily yields the discrepancy, and in particular, without having to deal with so‐called free‐riders.