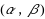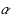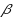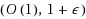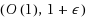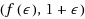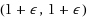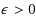New Approximation Algorithms for the Unsplittable Capacitated Facility Location Problem

In this paper, we consider the Unsplittable (hard) Capacitated Facility Location Problem (UCFLP) with uniform capacities and present new approximation algorithms for it. This problem is a generalization of the classical facility location problem where each facility can serve at most u units of demand and each client must be served by exactly one facility. This problem is motivated by its applications in many practical problems including supply chain problems of indivisible goods (Verter in Foundations of location analysis, chapter 2. International series in operations research and management science. Springer, Berlin, 2011) and the assignment problem in the content distribution networks (Bateni and Hajiaghayi in Proceedings of the nineteenth annual ACM‐SIAM symposium on discrete algorithms, pp 805–814, 2009). While there are several approximation algorithms for the soft capacitated version of this problem (in which one can open multiple copies of each facility) or the splittable version (in which the demand of each client can be divided to be served by multiple open facilities), there are very few results for the UCFLP. It is known that it is NP‐hard to approximate this problem within any factor without violating the capacities. So we consider bicriteria 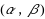$(\mathit{\alpha },\mathit{\beta })$ ‐approximations where the algorithm returns a solution whose cost is within factor 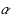$\mathit{\alpha }$ of the optimum and violates the capacity constraints within factor 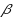$\mathit{\beta }$ . Shmoys et al. (Proceedings of the twenty‐ninth annual ACM symposium on theory of computing, pp 265–274, 1997) were the first to consider this problem and gave a (9, 4)‐approximation. Later results imply (O(1), 2)‐approximations, however, no constant factor approximation is known with capacity violation of less than 2. We present a framework for designing bicriteria approximation algorithms for this problem and show two new approximation algorithms with factors (9, 3 / 2) and (29.315, 4 / 3). These are the first algorithms with constant approximation in which the violation of capacities is below 2. The heart of our algorithm is a reduction from the UCFLP to a restricted version of the problem. One feature of this reduction is that any 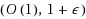$(O(1),1+\mathit{ϵ})$ ‐approximation for the restricted version implies an 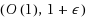$(O(1),1+\mathit{ϵ})$ ‐approximation for the UCFLP and we believe our techniques might be useful towards finding such approximations or perhaps 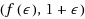$(f(\mathit{ϵ}),1+\mathit{ϵ})$ ‐approximation for the UCFLP for some function f. 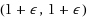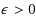In addition, we present a quasi‐polynomial time $(1+\mathit{ϵ},1+\mathit{ϵ})$ ‐approximation for the (uniform) UCFLP in Euclidean metrics, for any constant $\mathit{ϵ}>0$ .