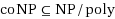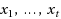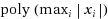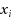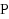Drucker (Proceedings of the 53rd annual symposium on foundations of computer science (FOCS), pp 609–618. doi: 10.1109/FOCS.2012.71" TargetType="DOI"/>
, 2012) proved the following result: Unless the unlikely complexity‐theoretic collapse
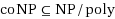 occurs, there is no AND‐compression for SAT. The result has implications for the compressibility and kernelizability of a whole range of NP‐complete parameterized problems. We present a streamlined proof of Drucker’s theorem. An AND‐compression is a deterministic polynomial‐time algorithm that maps a set of SAT‐instances
occurs, there is no AND‐compression for SAT. The result has implications for the compressibility and kernelizability of a whole range of NP‐complete parameterized problems. We present a streamlined proof of Drucker’s theorem. An AND‐compression is a deterministic polynomial‐time algorithm that maps a set of SAT‐instances
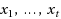 to a single SAT‐instance y of size
to a single SAT‐instance y of size
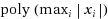 such that y is satisfiable if and only if all
such that y is satisfiable if and only if all
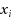 are satisfiable. The ‘AND’ in the name stems from the fact that the predicate ‘y is satisfiable’ can be written as the AND of all predicates ‘
are satisfiable. The ‘AND’ in the name stems from the fact that the predicate ‘y is satisfiable’ can be written as the AND of all predicates ‘
 is satisfiable’. Drucker’s theorem complements the result by Bodlaender et al. (J Comput Syst Sci 75:423–434, 2009) and Fortnow and Santhanam (J Comput Syst Sci 77:91–106, 2011), who proved the analogous statement for OR‐compressions, and Drucker’s proof not only subsumes their result but also extends it to randomized compression algorithms that are allowed to have a certain probability of failure. Drucker (Proceedings of the 53rd annual symposium on foundations of computer science (FOCS), pp 609–618. doi: 10.1109/FOCS.2012.71" TargetType="DOI"/>
, 2012) presented two proofs: The first uses information theory and the minimax theorem from game theory, and the second is an elementary, iterative proof that is not as general. In our proof, we realize the iterative structure as a generalization of the arguments of Ko (J Comput Syst Sci 26:209–211, 1983) for
is satisfiable’. Drucker’s theorem complements the result by Bodlaender et al. (J Comput Syst Sci 75:423–434, 2009) and Fortnow and Santhanam (J Comput Syst Sci 77:91–106, 2011), who proved the analogous statement for OR‐compressions, and Drucker’s proof not only subsumes their result but also extends it to randomized compression algorithms that are allowed to have a certain probability of failure. Drucker (Proceedings of the 53rd annual symposium on foundations of computer science (FOCS), pp 609–618. doi: 10.1109/FOCS.2012.71" TargetType="DOI"/>
, 2012) presented two proofs: The first uses information theory and the minimax theorem from game theory, and the second is an elementary, iterative proof that is not as general. In our proof, we realize the iterative structure as a generalization of the arguments of Ko (J Comput Syst Sci 26:209–211, 1983) for
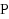 ‐selective sets, which use the fact that tournaments have dominating sets of logarithmic size. We generalize this fact to hypergraph tournaments. Our proof achieves the full generality of Drucker’s theorem, avoids the minimax theorem, and restricts the use of information theory to a single, intuitive lemma about the average noise sensitivity of compressive maps. To prove this lemma, we use the same information‐theoretic inequalities as Drucker.
‐selective sets, which use the fact that tournaments have dominating sets of logarithmic size. We generalize this fact to hypergraph tournaments. Our proof achieves the full generality of Drucker’s theorem, avoids the minimax theorem, and restricts the use of information theory to a single, intuitive lemma about the average noise sensitivity of compressive maps. To prove this lemma, we use the same information‐theoretic inequalities as Drucker.