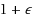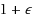Matroid and Knapsack Center Problems

In the classic k‐center problem, we are given a metric graph, and the objective is to select k nodes as centers such that the maximum distance from any vertex to its closest center is minimized. In this paper, we consider two important generalizations of k‐center, the matroid center problem and the knapsack center problem. Both problems are motivated by recent content distribution network applications. Our contributions can be summarized as follows: (1) We consider the matroid center problem in which the centers are required to form an independent set of a given matroid. We show this problem is NP‐hard even on a line. We present a 3‐approximation algorithm for the problem on general metrics. We also consider the outlier version of the problem where a given number of vertices can be excluded as outliers from the solution. We present a 7‐approximation for the outlier version. (2) We consider the (multi‐)knapsack center problem in which the centers are required to satisfy one (or more) knapsack constraint(s). It is known that the knapsack center problem with a single knapsack constraint admits a 3‐approximation. However, when there are at least two knapsack constraints, we show this problem is not approximable at all. To complement the hardness result, we present a polynomial time algorithm that gives a 3‐approximate solution such that one knapsack constraint is satisfied and the others may be violated by at most a factor of 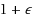$1+\mathit{ϵ}$ . 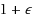We also obtain a 3‐approximation for the outlier version that may violate the knapsack constraint by $1+\mathit{ϵ}$ .