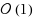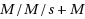Optimality gap of asymptotically derived prescriptions in queueing systems

In complex systems, it is quite common to resort to approximations when optimizing system performance. These approximations typically involve selecting a particular system parameter and then studying the performance of the system as this parameter grows without bound. In such an asymptotic regime, we prove that if the approximation to the objective function is accurate up to $\mathcal{O}(1)$ , then under some regularity conditions, the prescriptions that are derived from this approximation are o(1)‐optimal, i.e., their optimality gap is asymptotically zero. A consequence of this result is that the well‐known square‐root staffing rules for capacity sizing in M / M / s and $M/M/s+M$ queues to minimize the sum of linear expected steady‐state customer waiting costs and linear capacity costs are o(1)‐optimal. We also discuss extensions of this result for the case of nonlinear customer waiting costs in these systems.