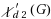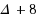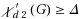| Article ID: | iaor20162376 |
| Volume: | 65 |
| Issue: | 2 |
| Start Page Number: | 351 |
| End Page Number: | 367 |
| Publication Date: | Jun 2016 |
| Journal: | Journal of Global Optimization |
| Authors: | Du Ding-Zhu, Wang Yanwen, Wang Weifan, Wang Yiqiao, Huang Danjun |
| Keywords: | graphs, heuristics |
Given a graph