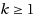This is the second part of a survey on the infinite group problem, an infinite‐dimensional relaxation of integer linear optimization problems introduced by Ralph Gomory and Ellis Johnson in their groundbreaking papers titled Some continuous functions related to corner polyhedra I, II (Math Program 3:23–85, 1972a; Math Program 3:359–389, 1972b). The survey presents the infinite group problem in the modern context of cut generating functions. It focuses on the recent developments, such as algorithms for testing extremality and breakthroughs for the k‐row problem for general
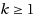that extend previous work on the single‐row and two‐row problems. The survey also includes some previously unpublished results; among other things, it unveils piecewise linear extreme functions with more than four different slopes. An interactive companion program, implemented in the open‐source computer algebra package Sage, provides an updated compendium of known extreme functions.
