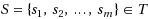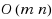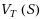| Article ID: | iaor2013789 |
| Volume: | 113 |
| Issue: | 4 |
| Start Page Number: | 132 |
| End Page Number: | 136 |
| Publication Date: | Feb 2013 |
| Journal: | Information Processing Letters |
| Authors: | Liu Yong-Jin, Tang Kai |
| Keywords: | graphs, heuristics |
We study the combinatorial complexity of Voronoi diagram of point sites on a general triangulated 2‐manifold surface, based on the geodesic metric. Given a triangulated 2‐manifold