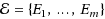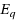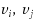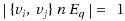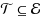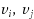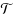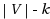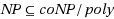(Non-)existence of polynomial kernels for the Test Cover problem

The input of the Test Cover problem consists of a set V of vertices, and a collection 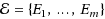$\mathcal{E}=\{E_1,\dots ,E_m\}$ of distinct subsets of V, called tests. A test 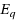$E_q$ separates a pair 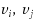$v_i,v_j$ of vertices if 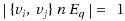$|\{v_i,v_j\}n{E}_q|=1$ . A subcollection 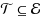$\mathcal{T}\subseteq \mathcal{E}$ is a test cover if each pair 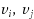$v_i,v_j$ of distinct vertices is separated by a test in 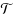$\mathcal{T}$ . The objective is to find a test cover of minimum cardinality, if one exists. This problem is NP‐hard. We consider two parameterizations of the Test Cover problem with parameter k: (a) decide whether there is a test cover with at most k tests, (b) decide whether there is a test cover with at most 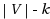$|V|‐k$ tests. Both parameterizations are known to be fixed‐parameter tractable. We prove that none have a polynomial size kernel unless 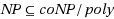$\mathit{NP}\subseteq \mathit{coNP}/\mathit{poly}$ . Our proofs use the cross‐composition method recently introduced by Bodlaender et al. (2011) and parametric duality introduced by Chen et al. (2005). The result for the parameterization (a) was an open problem (private communications with Henning Fernau and Jiong Guo, Jan.–Feb. 2012). We also show that the parameterization (a) admits a polynomial size kernel if the size of each test is upper‐bounded by a constant.