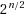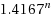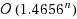| Article ID: | iaor20132359 |
| Volume: | 113 |
| Issue: | 8 |
| Start Page Number: | 276 |
| End Page Number: | 279 |
| Publication Date: | Apr 2013 |
| Journal: | Information Processing Letters |
| Authors: | Krzywkowski Marcin |
| Keywords: | sets |
We disprove a conjecture by Skupien that every tree of order