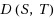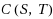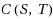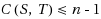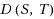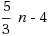As well known the rotation distance
 between two binary trees S, T of n vertices is the minimum number of rotations of pairs of vertices to transform S into T. We introduce the new operation of chain rotation on a tree, involving two chains of vertices, that requires changing exactly three pointers in the data structure as for a standard rotation, and define the corresponding chain distance
between two binary trees S, T of n vertices is the minimum number of rotations of pairs of vertices to transform S into T. We introduce the new operation of chain rotation on a tree, involving two chains of vertices, that requires changing exactly three pointers in the data structure as for a standard rotation, and define the corresponding chain distance
 . As for
. As for
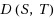 , no polynomial time algorithm to compute
, no polynomial time algorithm to compute
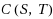 is known. We prove a constructive upper bound and an analytical lower bound on
is known. We prove a constructive upper bound and an analytical lower bound on
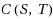 based on the number of maximal chains in the two trees. More precisely we prove the general upper bound
based on the number of maximal chains in the two trees. More precisely we prove the general upper bound
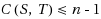 and we show that there are pairs of trees for which this bound is tight. No similar result is known for
and we show that there are pairs of trees for which this bound is tight. No similar result is known for
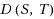 where the best upper and lower bounds are
where the best upper and lower bounds are
 and
and
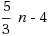 respectively.
respectively.