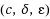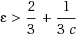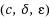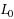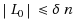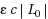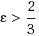| Article ID: | iaor20131665 |
| Volume: | 113 |
| Issue: | 7 |
| Start Page Number: | 225 |
| End Page Number: | 228 |
| Publication Date: | Apr 2013 |
| Journal: | Information Processing Letters |
| Authors: | Viderman Michael |
| Keywords: | coding system |
Feldman et al. (2007) [3] proved that LP decoding corrects