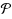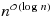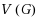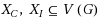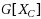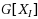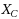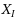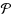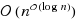Split Vertex Deletion meets Vertex Cover: New fixed-parameter and exact exponential-time algorithms

In the Split Vertex Deletion problem, given a graph G and an integer k, we ask whether one can delete k vertices from the graph G to obtain a split graph (i.e., a graph, whose vertex set can be partitioned into two sets: one inducing a clique and the second one inducing an independent set). In this paper we study exact (exponential‐time) and fixed‐parameter algorithms for Split Vertex Deletion.

We show that, up to a factor quasipolynomial in k and polynomial in n, the Split Vertex Deletion problem can be solved in the same time as the well‐studied Vertex Cover problem. By plugging in the currently best fixed‐parameter algorithm for Vertex Cover due to Chen et al. [Theor. Comput. Sci. 411 (40–42) (2010) 3736–3756], we obtain an algorithm that solves Split Vertex Deletion in time $\mathcal{O}({1.2738}^k{k}^{\mathcal{O}(\log k)}+n^3)$ .

We show that all maximal induced split subgraphs of a given n‐vertex graph can be listed in $\mathcal{O}(3^{n/3}{n}^{\mathcal{O}(\log n)})$ time.

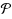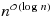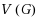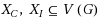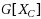To achieve our goals, we prove the following structural result that may be of independent interest: for any graph G we may compute a family $\mathcal{P}$ of size $n^{\mathcal{O}(\log n)}$ containing partitions of $V(G)$ into two parts, such that for any two disjoint sets $X_C,X_I\subseteq V(G)$ where $G[X_C]$ is a clique and 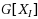$G[X_I]$ is an independent set, there is a partition in 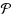$\mathcal{P}$ which contains all vertices of 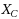$X_C$ on one side and all vertices of 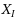$X_I$ on the other. Moreover, the family 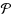$\mathcal{P}$ can be enumerated in 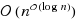$\mathcal{O}(n^{\mathcal{O}(\log n)})$ time.