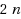Maximal- and minimal symmetric solutions of fully fuzzy linear systems

In this paper, we shall propose a new method to obtain symmetric solutions of a fully fuzzy linear system (FFLS) based on a 1‐cut expansion. To this end, we solve the 1‐cut of a FFLS (in the present paper, we assumed that the 1‐cut of a FFLS is a crisp linear system or equivalently, the matrix coefficient and right hand side have triangular shapes), then some unknown symmetric spreads are allocated to each row of a 1‐cut of a FFLS. So, after some manipulations, the original FFLS is transformed to solving $2n$ linear equations to find the symmetric spreads. However, our method always give us a fuzzy number vector solution. Moreover, using the proposed method leads to determining the maximal‐ and minimal symmetric solutions of the FFLS which are placed in a Tolerable Solution Set and a Controllable Solution Set, respectively. However, the obtained solutions could be interpreted as bounded symmetric solutions of the FFLS which are useful for a large number of multiplications existing between two fuzzy numbers. Finally, some numerical examples are given to illustrate the ability of the proposed method.