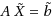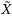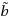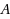Fuzzy symmetric solutions of fuzzy linear systems

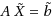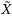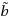In this paper, we propose a simple and practical method to solve a fuzzy linear system $A\tilde{X}=\tilde{b}$ , where $\tilde{X}$ and $\tilde{b}$ are fuzzy triangular vectors with non‐zero spreads and matrix 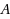$A$ is nonsingular with real coefficients. The aim of this paper is twofold. First, we obtain the crisp solution of a fuzzy linear system. To this end, we solve the 1‐cut of a fuzzy linear system. Second, we allocate some unknown symmetric spreads to any rows of fuzzy linear system in 1‐cut position. Thus, a fuzzy linear system in 1‐cut will be transformed to a system of interval equations. The symmetric spreads of each element of a fuzzy vector solution are derived by solving such an interval system. Moreover, based on the obtained symmetric spreads we derive three types of solutions. However, one of the mentioned spreads has pessimistic/optimistic attitude that is determined with a decision maker. It seems that such a solution is a connection solution between Tolerable Solution Set (TSS) and Controllable Solution Set (CSS). Also, we derive the maximal solution and the minimal solution of an original fuzzy linear system which are placed in TSS and CSS, respectively. Finally, some numerical examples are given to illustrate the efficiency and ability of the proposed method.