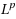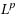An application of Taylor series in the approximation of solutions to stochastic differential equations with time-dependent delay

The subject of this paper is the analytic approximation method for solving stochastic differential equations with time‐dependent delay. Approximate equations are defined on equidistant partitions of the time interval, and their coefficients are Taylor approximations of the coefficients of the initial equation. It will be shown, without making any restrictive assumption for the delay function, that the approximate solutions converge in $L^p$ ‐norm and with probability 1 to the solution of the initial equation. Also, the rate of the $L^p$ convergence increases when the degrees in the Taylor approximations increase, analogously to what is found in real analysis. At the end, a procedure will be presented which allows the application of this method, with the assumption of continuity of the delay function.