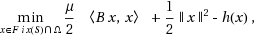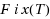| Article ID: | iaor20114473 |
| Volume: | 235 |
| Issue: | 12 |
| Start Page Number: | 3515 |
| End Page Number: | 3526 |
| Publication Date: | Apr 2011 |
| Journal: | Journal of Computational and Applied Mathematics |
| Authors: | Kang Shin Min, Yao Yonghong, Liou Yeong-Cheng |
| Keywords: | heuristics |
In this paper, we study the following minimization problem