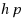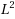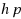| Article ID: | iaor20114460 |
| Volume: | 235 |
| Issue: | 12 |
| Start Page Number: | 3435 |
| End Page Number: | 3454 |
| Publication Date: | Apr 2011 |
| Journal: | Journal of Computational and Applied Mathematics |
| Authors: | Chen Yanping, Lin Yijie |
| Keywords: | optimization, programming: convex |
In this paper, we present a posteriori error analysis for