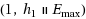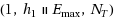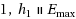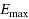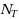In this paper the problem of minimizing maximum earliness on a single machine with an unavailability period
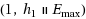 and also the same problem with simultaneous minimization of the two criteria of maximum earliness and number of tardy jobs
and also the same problem with simultaneous minimization of the two criteria of maximum earliness and number of tardy jobs
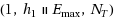 are studied. It is shown that the problem
are studied. It is shown that the problem
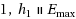 is NP‐hard. For this problem a branch and bound approach is proposed which is based on a binary search tree. Proposing a heuristic algorithm named MMST, lower bound and efficient dominance rules, results in some instances with up to 3000 jobs being solved. The purpose in the problem
is NP‐hard. For this problem a branch and bound approach is proposed which is based on a binary search tree. Proposing a heuristic algorithm named MMST, lower bound and efficient dominance rules, results in some instances with up to 3000 jobs being solved. The purpose in the problem
 is to find the set of efficient solutions, i.e. the Pareto frontier. For this reason, for each measure
is to find the set of efficient solutions, i.e. the Pareto frontier. For this reason, for each measure
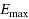 and
and
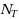 at first changes domain are calculated. A heuristic algorithm named PH and a branch and bound approach are developed to solve the problem. Proposing a lower bound and some dominance rules resulted in 96.4% of instances being solved optimally which proves the efficiency of the proposed method.
at first changes domain are calculated. A heuristic algorithm named PH and a branch and bound approach are developed to solve the problem. Proposing a lower bound and some dominance rules resulted in 96.4% of instances being solved optimally which proves the efficiency of the proposed method.