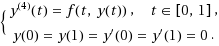| Article ID: | iaor20119232 |
| Volume: | 62 |
| Issue: | 6 |
| Start Page Number: | 2639 |
| End Page Number: | 2647 |
| Publication Date: | Sep 2011 |
| Journal: | Computers and Mathematics with Applications |
| Authors: | Zhai Chengbo, Song Ruipeng, Han Qianqian |
| Keywords: | differential equations |
The purpose of this paper is to investigate the existence and the uniqueness of symmetric positive solutions for a class of fourth‐order boundary value problem: