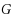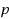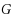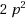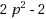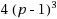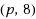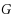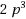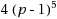| Article ID: | iaor20119214 |
| Volume: | 62 |
| Issue: | 6 |
| Start Page Number: | 2472 |
| End Page Number: | 2479 |
| Publication Date: | Sep 2011 |
| Journal: | Computers and Mathematics with Applications |
| Authors: | Bretto Alain, Faisant Alain, Gillibert Luc |
| Keywords: | optimization |
Constructing regular graphs with a given girth, a given degree and the fewest possible vertices is hard. This problem is called the cage graph problem and has some links with the error code theory.