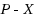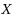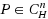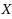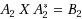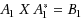| Article ID: | iaor20119210 |
| Volume: | 62 |
| Issue: | 6 |
| Start Page Number: | 2424 |
| End Page Number: | 2433 |
| Publication Date: | Sep 2011 |
| Journal: | Computers and Mathematics with Applications |
| Authors: | Li Ying, Zhang Fengxia, Zhao Jianli |
| Keywords: | matrices |
In this paper, we give some closed‐form formulas for calculating maximal and minimal ranks and inertias of