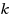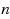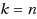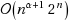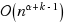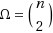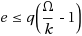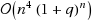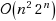| Article ID: | iaor20118233 |
| Volume: | 62 |
| Issue: | 4 |
| Start Page Number: | 1828 |
| End Page Number: | 1837 |
| Publication Date: | Aug 2011 |
| Journal: | Computers and Mathematics with Applications |
| Authors: | Schott Ren, Staples G Stacey |
| Keywords: | matrices |
Nilpotent adjacency matrix methods are employed to count