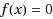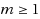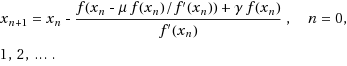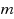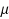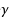| Article ID: | iaor20118210 |
| Volume: | 62 |
| Issue: | 4 |
| Start Page Number: | 1634 |
| End Page Number: | 1640 |
| Publication Date: | Aug 2011 |
| Journal: | Computers and Mathematics with Applications |
| Authors: | Kim Young Ik, Geum Young Hee |
| Keywords: | programming: nonlinear |
A second‐derivative‐free iteration method is proposed below for finding a root of a nonlinear equation