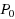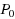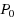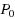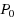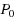Traffic control and route choice: Capacity maximisation and stability

This paper presents idealised natural general and more special dynamical models of day‐to‐day re‐routeing and of day to day green‐time response. Both green‐time response models are based on the responsive control policy 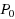$P_0$ introduced in Smith (1979a, b, c, 1987). It is shown that, for any steady feasible demand within a flow model, if the general day to day re‐routeing model is combined with the general day to day green‐time response model then under natural conditions any (flow, green‐time) solution trajectory cannot leave the region of supply‐feasible (flow, green‐time) pairs and costs are bounded. It is also shown that if the more special re‐routeing model is combined with the more special green‐time response model then every (flow, green‐time) solution trajectory converges to a non‐empty set of Wardrop equilibria consistent with the 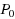$P_0$ control policy. Throughput is maximised in two senses. Given any constant feasible demand; this demand is (i) met as any routeing/green‐time trajectory evolves (following either the general or the more special model) and also (ii) met at a Wardrop equilibrium which is consistent with the 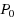$P_0$ green‐time response. (This is guaranteed to exist, under natural conditions.) The paper then considers control models with explicit queues, and provides a statement of simple ‘pressure driven’ responsive control policies, where cycle times are all fixed. In these policies stage pressures are given functions of flows, queues and green‐times. Finally the paper considers modified Varaiya (2013a, b) and Le et al. (2015) pressure‐driven responsive controls on a very simple one junction network. It is shown that (with each of these two modified policies) there is a steady demand within the capacity of the network for which there is no Wardrop equilibrium consistent with the policy. With each of these two modified policies on this simple network, as natural routeing/green‐time trajectories evolve queues and delays are unbounded. It is shown that, in contrast, responsive 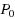$P_0$ on this simple network does maximise throughput at a quasi‐dynamic user equilibrium consistent with 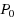$P_0$ ; queues and delays remain bounded in natural dynamical evolutions in this case. It is to be expected that this 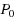$P_0$ result may be extended to allow for certain time‐varying demands on a much wider variety of networks, including dynamic networks; to show that this is indeed the case is a challenge for the future.