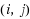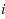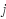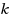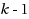| Article ID: | iaor201530302 |
| Volume: | 18 |
| Issue: | 11 |
| Start Page Number: | 168 |
| End Page Number: | 188 |
| Publication Date: | Nov 2015 |
| Journal: | Discrete Optimization |
| Authors: | Smith J Cole, Hicks Illya V, Sonuc Sibel B |
| Keywords: | graphs, heuristics |
Given an undirected graph, a bramble is a set of connected subgraphs (called bramble elements) such that every pair of subgraphs either contains a common node, or such that an edge