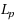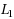Geometric versions of the three-dimensional assignment problem under general norms

We discuss the computational complexity of special cases of the three‐dimensional (axial) assignment problem where the elements are points in a Cartesian space and where the cost coefficients are the perimeters of the corresponding triangles measured according to a certain norm. (All our results also carry over to the corresponding special cases of the three‐dimensional matching problem.) The minimization version is NP‐hard for every norm, even if the underlying Cartesian space is 2‐dimensional. The maximization version is polynomially solvable, if the dimension of the Cartesian space is fixed and if the considered norm has a polyhedral unit ball. If the dimension of the Cartesian space is part of the input, the maximization version is NP‐hard for every $L_p$ norm; in particular the problem is NP‐hard for the Manhattan norm $L_1$ and the Maximum norm $L_{\infty }$ which both have polyhedral unit balls.