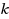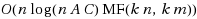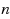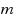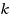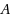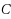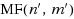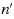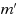L-extendable functions and a proximity scaling algorithm for minimum cost multiflow problem

In this paper, we develop a theory of new classes of discrete convex functions, called L‐extendable functions and alternating L‐convex functions, defined on the product of trees. We establish basic properties for optimization: a local‐to‐global optimality criterion, the steepest descend algorithm by successive 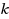$k$ ‐submodular function minimizations, the persistency property, and the proximity theorem. Our theory is motivated by minimum cost free multiflow problem. To this problem, Goldberg and Karzanov gave two combinatorial weakly polynomial time algorithms based on capacity and cost scalings, without explicit running time. As an application of our theory, we present a new simple polynomial proximity scaling algorithm to solve minimum cost free multiflow problem in 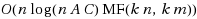$O(nlog\left(nAC\right)\mathrm{MF}(kn,km))$ time, where 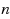$n$ is the number of nodes, 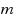$m$ is the number of edges, 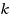$k$ is the number of terminals, 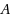$A$ is the maximum of edge‐costs, 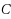$C$ is the total sum of edge‐capacities, and 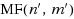$\mathrm{MF}(n^{\text{'}},m^{\text{'}})$ denotes the time complexity to find a maximum flow in a network of 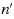$n^{\text{'}}$ nodes and 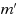$m^{\text{'}}$ edges. Our algorithm is designed to solve, in the same time complexity, a more general class of multiflow problems, minimum cost node‐demand multiflow problem, and is the first combinatorial polynomial time algorithm to this class of problems. We also give an application to network design problem.