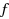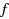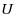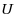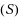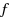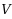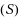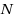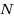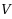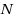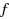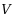Optimization over the Pareto outcome set associated with a convex bi-objective optimization problem: theoretical results, deterministic algorithm and application to the stochastic case

Our paper consists of two main parts. In the first one, we deal with the deterministic problem of minimizing a real valued function 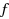$f$ over the Pareto outcome set associated with a deterministic convex bi‐objective optimization problem (BOP), in the particular case where 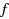$f$ depends on the objectives of (BOP), i.e. we optimize over the Pareto set in the outcome space. In general, the optimal value 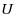$U$ of such a kind of problem cannot be computed directly, so we propose a deterministic outcome space algorithm whose principle is to give at every step a range (lower bound, upper bound) that contains 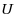$U$ . Then we show that for any given error bound, the algorithm terminates in a finite number of steps. In the second part of our paper, in order to handle also the stochastic case, we consider the situation where the two objectives of (BOP) are given by expectations of random functions, and we deal with the stochastic problem 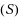$(S)$ of minimizing a real valued function 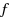$f$ over the Pareto outcome set associated with this Stochastic bi‐objective Optimization Problem (SBOP). Because of the presence of random functions, the Pareto set associated with this type of problem cannot be explicitly given, and thus it is not possible to compute the optimal value 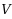$V$ of problem 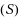$(S)$ . That is why we consider a sequence of Sample Average Approximation problems (SAA‐ 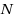$N$ , where 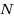$N$ is the sample size) whose optimal values converge almost surely to 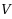$V$ as the sample size 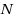$N$ goes to infinity. Assuming 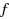$f$ nondecreasing, we show that the convergence rate is exponential, and we propose a confidence interval for 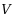$V$ . Finally, some computational results are given to illustrate the paper.