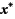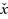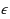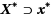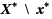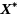Some observations on exclusion regions in branch and bound algorithms

In branch and bound algorithms for constrained global optimization, an acceleration technique is to construct regions 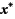${‐{x}}^{\ast }$ around local optimizing points 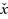$\check{x}$ , then delete these regions from further search. The result of the algorithm is then a list of those small regions in which all globally optimizing points must lie. If the constructed regions are too small, the algorithm will not be able to easily reject adjacent regions in the search, while, if the constructed regions are too large, the set of optimizing points is not known accurately. We briefly review previous methods of constructing boxes about approximate optimizing points. We then derive a formula for determining the size of a constructed solution‐containing region, depending on a small radius 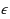$\mathit{ϵ}$ , and of constructing a containing box 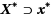${‐{X}}^{\ast }\supset {‐{x}}^{\ast }$ such that all points in 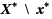${‐{X}}^{\ast }\backslash {‐{x}}^{\ast }$ are proven to be infeasible, without the need to actually process them in the branch and bound algorithm. The construction differs in its motivation and concept from previous methods of constructing such boxes 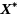${‐{X}}^{\ast }$ . It may be possible to use this technique to reduce the large amount of processing branch and bound algorithms typically require to fathom regions adjacent to optimizing points, and to obtain more accurate bounds on solution sets.