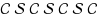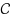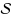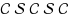Optimal curvature and gradient-constrained directional cost paths in 3-space

In the design of underground tunnel layout, the development cost is often dependent on the direction of the tunnel at each point due to directional ground fracturing. This paper considers the problem of finding a minimum cost curvature‐constrained path between two directed points in 3‐space, where the cost at every point along the path depends on the instantaneous direction. This anisotropic behaviour of the cost models the development cost of a tunnel in ground with faulting planes that are almost vertical. The main result we prove in this paper is that there exists an optimal path of the form $\mathcal{C}\mathcal{S}\mathcal{C}\mathcal{S}\mathcal{C}\mathcal{S}\mathcal{C}$ (or a degeneracy), where $\mathcal{C}$ represents a segment of a helix with unit radius and $\mathcal{S}$ represents a straight line segment. This generalises a previous result that in the restriction of the problem to the horizontal plane there always exists a path of the form $\mathcal{C}\mathcal{S}\mathcal{C}\mathcal{S}\mathcal{C}$ or a degeneracy which is optimal. We also prove some key structural results which are necessary for creating an algorithm which can construct an optimal path between a given pair of directed points in 3‐space with a prescribed directional cost function.