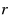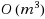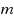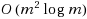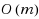| Article ID: | iaor201526125 |
| Volume: | 62 |
| Issue: | 2 |
| Start Page Number: | 371 |
| End Page Number: | 389 |
| Publication Date: | Jun 2015 |
| Journal: | Journal of Global Optimization |
| Authors: | Brimberg Jack, Schbel Anita, Schieweck Robert |
| Keywords: | demand, location |
We generalize the classical median line location problem, where the sum of distances from a line to some given demand points is to be minimized, to a setting with