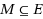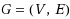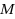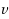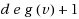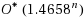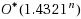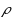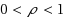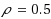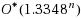An induced matching
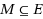 in a graph
in a graph
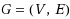 is a matching such that no two edges in
is a matching such that no two edges in
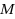 are joined by any third edge of the graph. The Maximum Induced Matching problem is to find an induced matching of maximum cardinality. It is NP‐hard. Branch‐and‐reduce algorithms proposed in the previous results for the Maximum Induced Matching problem use a standard branching rule: for a vertex
are joined by any third edge of the graph. The Maximum Induced Matching problem is to find an induced matching of maximum cardinality. It is NP‐hard. Branch‐and‐reduce algorithms proposed in the previous results for the Maximum Induced Matching problem use a standard branching rule: for a vertex
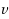 , it branches into
, it branches into
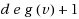 subproblems that either
subproblems that either
 is not an endvertex of any edge in
is not an endvertex of any edge in
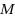 or
or
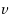 and one of its neighbor are endvertices of an edge in
and one of its neighbor are endvertices of an edge in
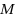 . In this paper, we give a simple branch‐and‐reduce algorithm consisting of a boundary condition, a reduction rule, and a branching rule. Especially, the branching rule only branches the original problem into two subproblems. When the algorithm meets the input instance satisfying the boundary condition, we reduce the Maximum Induced Matching problem to the Maximum Independent Set problem. By using the measure‐and‐conquer approach to analyze the running time of the algorithm, we show that this algorithm runs in time
. In this paper, we give a simple branch‐and‐reduce algorithm consisting of a boundary condition, a reduction rule, and a branching rule. Especially, the branching rule only branches the original problem into two subproblems. When the algorithm meets the input instance satisfying the boundary condition, we reduce the Maximum Induced Matching problem to the Maximum Independent Set problem. By using the measure‐and‐conquer approach to analyze the running time of the algorithm, we show that this algorithm runs in time
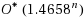 which is faster than previously known algorithms. By adding two branching rules in the simple exact algorithm, we obtain an
which is faster than previously known algorithms. By adding two branching rules in the simple exact algorithm, we obtain an
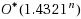 ‐time algorithm for the Maximum Induced Matching problem. Moreover, we give a moderately exponential time
‐time algorithm for the Maximum Induced Matching problem. Moreover, we give a moderately exponential time
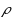 ‐approximation algorithm,
‐approximation algorithm,
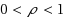 , for the Maximum Induced Matching problem. For
, for the Maximum Induced Matching problem. For
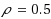 , the algorithm runs in time
, the algorithm runs in time
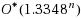 .
.