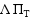Advanced algorithms for multidimensional sensitivity studies of large-scale air pollution models based on Sobol sequences

In this paper advanced variance‐based algorithms for global sensitivity analysis are studied. We consider efficient algorithms, such as Monte Carlo, quasi‐Monte Carlo (QMC) and scrambled quasi‐Monte Carlo algorithms based on Sobol sequences. Low discrepancy 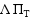$\Lambda {\Pi }_{{\rm T}}$ Sobol sequences are considered as a basis. Two other approaches are also analyzed. The first one is an efficient Monte Carlo (MC) algorithm for multidimensional integration based on modified Sobol sequences (MCA‐MSS) and proposed in an earlier work by some of the authors Dimov and Georgieva (2011) [28]. The second one is a randomized QMC algorithm proposed by Art Owen (1995) [20]. The procedure of randomization in the latter case is also known as Owen scrambling. The algorithms considered in this work are applied to sensitivity studies of air pollution levels calculated by the Unified Danish Eulerian Model (UNI‐DEM) to some chemical reaction rates. UNI‐DEM is chosen as a case study since it constitutes a typical large‐scale mathematical model in which the chemical reactions are adequately presented. Extensive numerical experiments are performed to support the theoretical studies and to analyze applicability of algorithms under consideration to various classes of problems. Conclusions about the applicability and efficiency of the algorithms under consideration are drawn.