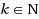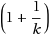Threshold-based preprocessing for approximating the weighted dense k-subgraph problem

Based on an application in forestry, we study the dense k‐subgraph problem: Given a parameter 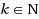$k\in ‐{N}$ and an undirected weighted graph G, the task is to find a subgraph of G with k vertices such that the sum of the weights of the induced edges is maximized. The problem is well‐known to be NP‐hard and difficult to approximate if the underlying graph does not satisfy the triangle inequality. In the present paper, we develop a fast preprocessing routine which results in a graph still containing a 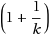$\left(1+\frac{1}{k}\right)$ ‐approximation for the problem. The key idea is to identify vertices which are of low interest to an optimal solution for the problem due to falling below a special ‘threshold’. Using this information, we initiate a chain‐reaction of vertex eliminations to reduce the number of vertices in the input graph without losing a lot of information. This graph reduction step runs in polynomial time. The success of this preprocessing step mainly depends on finding a large threshold, which ensures that many vertices can be removed. For this purpose, we devise an efficient algorithm which yields a provably optimal threshold. Finally, we present empiric studies for our application. Even though the graphs tied to our application in forestry have several hundred vertices and do not satisfy the triangle inequality, they exhibit special properties which yield a very favorable performance of our approach. The pruning step typically removes more than 90% of the vertices, and thus enables an optimal solution of the problem on the reduced graph.