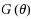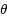| Article ID: | iaor201527023 |
| Volume: | 79 |
| Issue: | 5 |
| Start Page Number: | 1770 |
| End Page Number: | 1777 |
| Publication Date: | Jan 2009 |
| Journal: | Mathematics and Computers in Simulation |
| Authors: | Wang Lichun, Wang Xuan |
| Keywords: | Bayesian analysis, life expectancy, partial differential equations (PDE) |
This article considers the prediction problem of the life‐span of a system whose components connected in series and the lifetime of the components follows the exponential distribution with probability density