Some properties of a unit root test with multiple level shifts in the presence of Markov level shifts

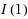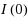This paper investigates the small sample properties of a unit root test under the framework of multiple level shifts when time series variables are $I(1)$ or $I(0)$ processes with Markov level shifts. In order to investigate these properties, we introduce a unit root test with multiple level shifts. The introduced test assumes that the unspecified number of level shifts may be larger than two but smaller than or equal to the maximum number of level shifts set a priori. The Monte Carlo simulations demonstrate that the properties of size and power of the test strongly depend on the transition probability and the degree of level shifts for Markov processes. When the level shifts are frequent and substantial, the test with multiple shifts contains size distortions and has low power as compared with the Dickey–Fuller test and the test designed for a single level shift. On the other hand, when the level shifts are persistent and substantial, the test with multiple shifts performs better than the Dickey–Fuller test and that designed for a single level shift.