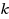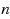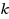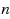| Article ID: | iaor201526322 |
| Volume: | 44 |
| Issue: | 2 |
| Start Page Number: | 295 |
| End Page Number: | 319 |
| Publication Date: | May 2015 |
| Journal: | International Journal of Game Theory |
| Authors: | Slinko Arkadii, Hameed Ali |
| Keywords: | hierarchical structure, weights |
Hierarchical simple games–both disjunctive and conjunctive–are natural generalizations of