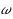Weak addition invariance and axiomatization of the weighted Shapley value

In this paper, we give a new axiomatization of the weighted Shapley value. We investigate the asymmetric property of the value by focusing on the invariance of payoff after the change in the worths of singleton coalitions. We show that if the worths change by the same amount, then the Shapley value is invariant. On the other hand, if the worths change with multiplying by a positive weight, then the weighted Shapley value with the positive weight is invariant. Based on the invariance, we formulate a new axiom, $\mathit{\omega }$ ‐Weak Addition Invariance. We prove that the weighted Shapley value is the unique solution function which satisfies $\mathit{\omega }$ ‐Weak Addition Invariance and Dummy Player Property. In the proof, we introduce a new basis of the set of all games. The basis has two properties. First, when we express a game by a linear combination of the basis, coefficients coincide with the weighted Shapley value. Second, the basis induces the null space of the weighted Shapley value. By generalizing the new axiomatization, we also axiomatize the family of weighted Shapley values.