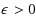| Article ID: | iaor201526181 |
| Volume: | 80 |
| Issue: | 3 |
| Start Page Number: | 197 |
| End Page Number: | 222 |
| Publication Date: | Jul 2015 |
| Journal: | Queueing Systems |
| Authors: | Stanford David, Xiong Yaofei, Murdoch Duncan |
| Keywords: | statistics: sampling |
In this paper, we explore algorithms for perfect and nearly perfect sampling from the stationary distribution of the waiting times in various Poisson arrival multi-class and multi-server queues with non-preemptive work-conserving service disciplines. The service duration distributions of these classes may be identical or may vary from class to class. The algorithms follow the idea of dominated coupling from the past (Kendall, 2000) and are variations on an algorithm of Sigman (2011). A coupled first come first serve queue is constructed for each work-conserving queue. When the service duration distributions do not vary, we achieve perfect simulation by finding times when the system is known to be totally idle. When the distributions differ, the totally idle times may be impossible to determine exactly, but we can achieve simulations with a specified error limit